Regresión logística
REGRESIÓN LOGÍSTICA
En la entrada anterior del aprendizaje automático hemos hablado sobre la regresión lineal. Esta técnica de aprendizaje automático consistía en entrenar un modelo/función (h) para que fuese capaz de predecir los valores de la salida, siempre generalizando. La regresión lineal es idea en problemas donde la salida es continua, pero no lo es tanto a la hora de clasificar los datos en grupos su actuación.
Por ello existe la regresión logística, que a diferencia de la regresión lineal, se centra en CLASIFICAR los datos en grupos o en discretizarlos.
 |
| Ejemplo de que como la regresión lineal no sirve para clasificar datos, la regresión logística sí que lo vale. |
Tal como se ha dicho, la regresión logística se usa para la clasificación de datos, pero ¿Cómo funciona realmente? ¿Qué diferencias tiene con la regresión lineal?
Existe para ello una función conocida como la FUNCIÓN SIGMOIDEA. Esta es capaz de transformar una función de valor arbitrario en una función más adecuada para la clasificación.
La función sigmoidea (h) se expresa de la siguiente forma:
Esta función tiene 2 formas: uno para cuando la salida es 1 y otra para cuando es 0.
Pero los matemáticos no se quedaron ahí, simplificaron y unificaron la fórmula para que se pudiera utilizar en cualquiera de los dos casos:
Clasificación
El objetivo de la clasificación es diferenciar los datos en dos o más grupos. Primero nos centraremos en la separación de los datos en dos grupos o, dicho de otra manera, en la DISCRETIZACIÓN BINARIA (1 o 0). Esto significa que, independientemente del dato que introduzcamos en la función, este nos tendrá que responder con un 1 o 0, esto es, si el dato es de un grupo o del otro. ¿Y conocemos alguna función que sea capaz de ello? La respuesta es sí, sino no, no estaríamos haciendo este blog.Existe para ello una función conocida como la FUNCIÓN SIGMOIDEA. Esta es capaz de transformar una función de valor arbitrario en una función más adecuada para la clasificación.
 |
| Sigma: Decimoctava letra del alfabeto griego. Se puede equiparar a la letra 'S' del alfabeto. Sigmoidea: Designa a todo aquello que presenta en su forma la apariencia de un sigma. |
Tal como hemos comentado tiene forma de sigma o de 'S':
 |
| Función sigmoidea: Función con forma de sigma, entre otras cosas sirve para la regresión logística. |
 |
| (h = función sigmoidea) |
Esta función (h) nos devuelve la probabilidad para que la salida (y) sea 1. Por ejemplo, si el resultado es que h = 0.7 significa que la probabilidad de que y = 1 es del 70%. La probabilidad de que sea 0 es el complemento del resultado de la probabilidad de que sea 1.
Por lo tanto, hasta ahora con la función sigmoidea tenemos una probabilidad de pertenencia a 1 o a 0. Pero hemos dicho que diferenciaba entre ambos con gran certeza ¿Qué nos falta entonces para que la clasificación sea discreta? Lo que falta es un límite de decisión.
Límite de decisión
Un límite de decisión, tal como expresa la palabra, es una frontera en el que se decide si un valor es de un lado o del otro, en nuestro caso 1 o 0. Para ello se define la siguiente función hipótesis: si el valor de la salida es mayor a 0.5 la salida es 1 y si es menor, es 0.
Mediante unas operaciones matemáticas que no se van a explicar aquí (y las cuales nos creeremos), y utilizando la función sigmoidea, la regresión logística se reduce a las siguientes igualdades:
Esto es, si la función de activación es positiva, la salida será 1, y si la función es negativa, 0. Por lo tanto el límite de decisión es una línea que separa el área donde 'y' es 1 o 0, y es creada por nuestra función de hipótesis.
Bien, ya sabemos como definir nuestra función hipótesis o modelo (h), pero ¿Cómo sabemos si es bueno? ¿Cómo sabemos si predice bien? ¡Eso es! Hay que utilizar una función de coste para comparar los valores de salida del modelo con las reales, y ver que tan bueno es el modelo (Si no os sabíais la respuesta pasaros a leer la anterior entrada de Regresión lineal). ;)
Función de coste para regresión logística
Tal como se hace con la regresión lineal, en la regresión logística también existe una función de coste que nos ayuda a ver las diferencias entre la realidad y el modelo. Pero, desafortunadamente no nos sirve la misma función de coste para la regresión logística.
Pero tranquilos, no pasa nada, los matemáticos ya resolvieron este problema creando una nueva función de coste para la regresión logística:
 |
| Se diferencia entre si la salida es 1 o 0, y se utilizan diferentes fórmulas para cada caso. |
 |
| Si se es demasiado complicado, recordad que es la misma función que la anterior. |
Gradiente de descenso
Para los que quieran una explicación, diríjanse a la entrada de Regresión lineal.
 |
| Misma función de minimización, diferente función a optimizar. |
Clasificación multiclase: One-vs-all
En los apartados anteriores, la clasificación de todos los modelos ha sido binaria (1 o 0), esto es, la salida pertenecía a un grupo o al otro. Pero al principio hemos comentado que la regresión logística es capaz también de diferenciar entre más de un grupo.
Cuando existen varias opciones de salida, lo que se hace es aplicar la regresión logística binaria a cada una. Es decir, se selecciona un grupo como principal y todos los grupos restantes se consideran de un mismo grupo mixto. Se aplica la regresión logística a estos dos grupos (el escogido y el grupo creado con los restantes) y se obtiene la función logística. Se repite esto con todos los grupos.
 |
| Representación de la clasificación multiclase: One-vs-all |
Básicamente, estamos eligiendo una clase y luego agrupando todas las demás en una segunda clase. Hacemos esto con cada clase, aplicando la regresión lineal binaria a cada una, y finalmente, la variable de entrada pertenecerá al grupo cuya hipótesis devuelva el valor de pertenencia más alto.
En resumidas cuentas, se elige un grupo y se compara con los demás, de ahí su nombre: One-vs-all.
En resumidas cuentas, se elige un grupo y se compara con los demás, de ahí su nombre: One-vs-all.
Para saber a que grupo pertenece un dato se calculan las probabilidades que tiene uno de pertenecer a una clase, o de ser positivo.
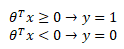
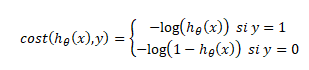


Comentarios
Publicar un comentario