Regresión lineal
REGRESIÓN LINEAL
En la entrada anterior hemos visto lo que es el aprendizaje automático y hemos aprendido que existen varios métodos de aprendizaje para una computadora o máquina. Pero ¿Cómo exactamente aprende una máquina? ¿Qué pasos hay que seguir para el aprendizaje? En esta entrada explicaremos cómo aprenden las máquinas y nos centraremos sobre todo en un método de aprendizaje: la Regresión lineal.
Tal como se explica en la entrada de Introducción al aprendizaje automático la regresión lineal es un tipo de aprendizaje supervisado, que parte de unos ejemplos conocidos de los cuales se conoce la relación entre la entrada y la salida, y con los que se puede conseguir la relación en forma de función.
 El mayor problema del aprendizaje supervisado es el entrenamiento. Este consiste en partir con un conjunto de datos con los cuales entrenar un algoritmo para que sea capaz de hacer relaciones entre la entrada y la salida. Es decir, que a partir de los valores de x (entrada) se crea un buen predictor (h) de los valores de y (salida).
El mayor problema del aprendizaje supervisado es el entrenamiento. Este consiste en partir con un conjunto de datos con los cuales entrenar un algoritmo para que sea capaz de hacer relaciones entre la entrada y la salida. Es decir, que a partir de los valores de x (entrada) se crea un buen predictor (h) de los valores de y (salida).
A este predictor (h) también se le conoce como modelo. Pero ¿Cómo sabemos una vez hecho el entrenamiento si el modelo es bueno o no? ¡Fácil! Basta con comparar el resultado real con el que ha predicho el modelo. Con una simple resta valdría :).
Bien, entonces supongamos que queremos crear un predictor, o modelo, de los precios de las casas en función al área que tienen. Cogemos unos ejemplos de estos datos, hacemos unos cálculos y obtenemos el modelo en forma de función (h). Ahora nos disponemos a probarlo, cogemos un dato nuevo de área, lo introducimos en el modelo y... ¡¿Pero que ha pasado?! ¡Si el modelo no predice bien el precio! No pasa nada... Se prueba con otro ejemplo y... Nada... Lo mismo...
Parece que el modelo predice bien algunos ejemplos, pero otros no tan bien. Esto se debe a que los parámetros del modelo se han ajustado bien a los ejemplos empleados para entrenarlo, pero no se ha ajustado a otros ejemplos externos. NO GENERALIZA.
Y os preguntaréis: ¿Qué se debe de hacer para solucionar este problema? Pues bien, de entre tantas soluciones, existe la minimización de la Función de Coste.
Entrenamiento del aprendizaje supervisado
 El mayor problema del aprendizaje supervisado es el entrenamiento. Este consiste en partir con un conjunto de datos con los cuales entrenar un algoritmo para que sea capaz de hacer relaciones entre la entrada y la salida. Es decir, que a partir de los valores de x (entrada) se crea un buen predictor (h) de los valores de y (salida).
El mayor problema del aprendizaje supervisado es el entrenamiento. Este consiste en partir con un conjunto de datos con los cuales entrenar un algoritmo para que sea capaz de hacer relaciones entre la entrada y la salida. Es decir, que a partir de los valores de x (entrada) se crea un buen predictor (h) de los valores de y (salida).A este predictor (h) también se le conoce como modelo. Pero ¿Cómo sabemos una vez hecho el entrenamiento si el modelo es bueno o no? ¡Fácil! Basta con comparar el resultado real con el que ha predicho el modelo. Con una simple resta valdría :).
Bien, entonces supongamos que queremos crear un predictor, o modelo, de los precios de las casas en función al área que tienen. Cogemos unos ejemplos de estos datos, hacemos unos cálculos y obtenemos el modelo en forma de función (h). Ahora nos disponemos a probarlo, cogemos un dato nuevo de área, lo introducimos en el modelo y... ¡¿Pero que ha pasado?! ¡Si el modelo no predice bien el precio! No pasa nada... Se prueba con otro ejemplo y... Nada... Lo mismo...
Parece que el modelo predice bien algunos ejemplos, pero otros no tan bien. Esto se debe a que los parámetros del modelo se han ajustado bien a los ejemplos empleados para entrenarlo, pero no se ha ajustado a otros ejemplos externos. NO GENERALIZA.
Y os preguntaréis: ¿Qué se debe de hacer para solucionar este problema? Pues bien, de entre tantas soluciones, existe la minimización de la Función de Coste.
Función de coste
La función de coste se utiliza en los problemas de regresión. Este predice el error que hay entre la salida del modelo h y el modelo real (y). También se le conoce como "Función del error al cuadrado" o "Error medio cuadrado".
La expresión matemática de la función de coste es la siguiente:
La expresión matemática de la función de coste es la siguiente:
Así puesto parece un churro que no hay quien lo entienda, pero si nos fijamos un poco no es más que una resta/una comparación. Es decir, la resta es la diferencia que hay entre el modelo y la realidad. Este error se eleva al cubo y se hace una suma con todos los ejemplos. Si se consigue que este valor sea el mínimo posible indicará que las variables del modelo son los que más se acercan a la realidad.
Por lo tanto, el objetivo del aprendizaje es minimizar la función de coste (J) para
que así los parámetros
hagan que el modelo (h) se
parezca lo más posible a la realidad (y). Si se consigue un buen predictor que sea capaz de generalizar (tanto con ejemplos de entrenamiento como con otros ejemplos), se dice que la ha sido bien entrenada.
Por lo tanto, hasta ahora tenemos una función de coste (J) que nos devuelve un valor, cuanto menor sea este valor mejor será nuestro modelo. Pero, ¿Cómo encontraremos los valores idóneos para que la función de coste sea mínima? Es decir, tenemos la herramienta que nos dice qué tan buena es nuestra aproximación, pero no tenemos un método para encontrar el mínimo. Bien pues, esta tarea se la encomendamos al Gradiente de Descenso.
Funciona de una manera muy simple. Imagínese que está en la cima de un monte y su objetivo es llegar al punto más bajo. Primero mira donde está y en qué dirección está la pendiente más empinada. Después de comparar todas las direcciones, escoge la más empinada y avanza unos metros en esa dirección. Se para y vuelve a mirar donde está, para elegir de nuevo el camino más empinado/rápido para llegar abajo. Así hasta llegar al mínimo del valle.
El gradiente de descenso funciona de la misma manera: se le facilitan al gradiente la función de la cual se quiere obtener el mínimo (Monte) y el parámetro a estimar (posición), este calcula la derivada de la función ("decide" en qué dirección está la mayor pendiente) para restar este valor al valor anterior (se mueve montaña abajo).
Por último queda COMBINAR TODO LO VISTO. Es decir, se coge la función de coste de la regresión lineal y se le aplica el algoritmo de gradiente de descenso, para así obtener los parámetros que harán que nuestra función sea lo más parecido posible a la realidad.
Al hacer esto se observa lo siguiente: en el caso de la regresión lineal, la función de coste de la regresión lineal tiene una forma convexa. Lo que significa que mediante el gradiente de descenso SIEMPRE convergerá al óptimo global, obteniendo siempre los parámetros ideales.
Para aclarar la previa afirmación se utilizará por última vez la metáfora de la montaña: NO HAY MONTAÑA PARA LA REGRESIÓN LINEAL, SOLAMENTE ES UN VALLE.
 |
| Entrenamiento en Machine learning, más mental que físico. |
Gradiente de descenso
Esta maravilla matemática sirve para encontrar el mínimo de una función, y en este caso en concreto lo utilizaremos para encontrar el mínimo de la función de coste (J).Funciona de una manera muy simple. Imagínese que está en la cima de un monte y su objetivo es llegar al punto más bajo. Primero mira donde está y en qué dirección está la pendiente más empinada. Después de comparar todas las direcciones, escoge la más empinada y avanza unos metros en esa dirección. Se para y vuelve a mirar donde está, para elegir de nuevo el camino más empinado/rápido para llegar abajo. Así hasta llegar al mínimo del valle.
 |
| Gradiente de descenso = Ir montaña abajo |
El gradiente de descenso funciona de la misma manera: se le facilitan al gradiente la función de la cual se quiere obtener el mínimo (Monte) y el parámetro a estimar (posición), este calcula la derivada de la función ("decide" en qué dirección está la mayor pendiente) para restar este valor al valor anterior (se mueve montaña abajo).
Puede parece que el gradiente soluciona el problema de minimización que teníamos, pero no es del todo cierto, hay que tener en cuenta que el gradiente de descenso no es perfecto y NO ASEGURA que:
- Pueda encontrar la mejor solución (Mínimos locales). Puede que cuando vayas montaña abajo te encuentres en un valle y creas que hayas llegado al punto más bajo, cuando en realidad existen otros valles que están aun más bajo.
- Pueda encontrar una solución en un número concreto de iteraciones (Tardar en llegar al óptimo). Puede pasar que se camine durante un buen tiempo antes de encontrar un buen valle.
- Pueda encontrar una solución (Problemas con la tasa de aprendizaje). Si al avanzar montaña abajo, se avanza mucha distancia sin mirar a donde se ha llegado, puede que se sobrepase el mínimo y se siga avanzando en la dirección errónea.
Gradiente de descenso para regresión lineal
Por último queda COMBINAR TODO LO VISTO. Es decir, se coge la función de coste de la regresión lineal y se le aplica el algoritmo de gradiente de descenso, para así obtener los parámetros que harán que nuestra función sea lo más parecido posible a la realidad.
Al hacer esto se observa lo siguiente: en el caso de la regresión lineal, la función de coste de la regresión lineal tiene una forma convexa. Lo que significa que mediante el gradiente de descenso SIEMPRE convergerá al óptimo global, obteniendo siempre los parámetros ideales.
| Gradiente de descenso en regresión lineal = Valle |
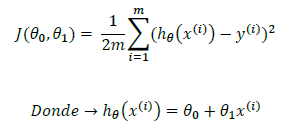




Comentarios
Publicar un comentario